Research Highlights

In antiferromagnets, the interplay of spin frustration and spin-lattice coupling has been extensively studied as the source of complex spin patterns and exotic magnetism. It is very interesting to study how ubiquitously the interplay leads to nontrivial phenomena. We demonstrated that, although neglected in the past, the spin-lattice coupling is essential to ferrimagnetic spinels as well. We performed ultrahigh-field magnetization measurements up to 110 T on a ferrimagnetic spinel, MnCr₂S₄, which was complemented by measurements of magnetostriction and sound velocities up to 60 T. Classical Monte Carlo calculations were performed to identify the complex high-field spin structures. Our minimal model incorporating spin-lattice coupling accounts for the experimental results and corroborates the complete phase diagram, including two new high-field phase transitions at 75 and 85 T. Magnetoelastic coupling induces striking effects: An extremely robust magnetization plateau is embedded between two unconventional spin-asymmetric phases. Ferrimagnetic spinels provide a new platform to study asymmetric and multiferroic phases stabilized by spin-lattice coupling.

• A. Miyata, H. Suwa, T. Nomura, L. Prodan, V. Felea, Y. Skourski, J. Deisenhofer, H.-A. Krug von Nidda, O. Portugall, S. Zherlitsyn, V. Tsurkan, J. Wosnitza, and A. Loidl Spin-lattice coupling in a ferrimagnetic spinel: Exotic H-T phase diagram of MnCr2S4 up to 110 T, Phys. Rev. B 101, 054432 (2020), preprint: arXiv:1911.12103

Crystal structure prediction has been known as one of the most difficult problems, and various prediction methods have been developed so far. Recently, joint optimization of experimental data and the theoretical potential energy calculation has been proposed. In that method, a combined cost function, a sum of reproducibility of experimental data and the potential energy, are optimized. However, combined cost function loses the information of the local minima of each cost functions. We developed a new optimization algorithm, Combined Optimization Method (COM), to overcome this difficulty. For example, it is known that the determination of crystal structure for SiO2 systems is quite difficult due to the existence of a lot of local minimum arrangements. By using the COM, we confirmed that the success rate of crystal structure prediction increases significantly.

• Naoto Tsujimoto, Daiki Adachi, Ryosuke Akashi, Synge Todo, Shinji Tsuneyuki, Crystal structure prediction supported by incomplete experimental data, Phys. Rev. Materials 2, 053801 (2018). (preprint: arXiv:1705.08613)

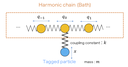Unlike the normal Langevin equation, the generalized Langevin equation, which deals with the memory effects, shows  various type diffusions depending on the memory function. Recently, the anomalous diffusion and the non-ergodicity have been actively studied in the terms of the generalized Langevin equation. There are, however, some confusions in the definition of the ergodicity and there are few analysis using physical models. We propose a new non-ergodic  model, which consists of harmonic oscillators, and analyze the model by the molecular dynamics, the exact diagonalization, and the analytical solution. We also reconsider the definition of the ergodicity, and clarify that the non-ergodicity observed in our model is caused by the localized mode.

• Fumihiro Ishikawa, Synge Todo, Localized Mode and Nonergodicity of a Harmonic Oscillator Chain, preprint: arXiv:1805.02923.

Machine learning (ML) is emerging as a promising tool to help model various types of many-body phenomena. A promising research area is the molecular dynamics (MD) of strongly correlated electron materials. While quantum MD methods based on the density functional theory have been successfully applied to a wide variety of materials, they have limited validity in their treatment of electron correlations. On the other hand, most of the many-body techniques, such as the dynamical mean-field theory, are computationally too costly for MD simulations. We showed that ML can be effective for building fast, linear-scaling MD potentials that capture correlated electron physics. Specifically, we used ML to enable large-scale Gutzwiller MD simulations of a liquid Hubbard model and studied the Mott metal-insulator transition. For the systems considered in the present study, ML is up to 6 orders of magnitude faster than direct quantum calculations. Our work opens a path toward a large-scale dynamical simulation of realistic models of correlated materials.

• Hidemaro Suwa, Justin S. Smith, Nicholas Lubbers, Cristian D. Batista, Gia-Wei Chern, and Kipton Barros
  Machine learning for molecular dynamics with strongly correlated electrons
  Phys. Rev. B 99, 161107(R) (2019). (preprint: arXiv:1811.01914)