Welcome to Todo Group

Computational Exploration of Quantum Many-Body Phenomena

To understand the state of matter, the many-body Schrödinger equation must be solved to obtain the partition function in statistical mechanics. However, even with the computational power of modern supercomputers, solving this equation completely is difficult. Therefore, a crucial issue in computational physics is reconstructing the original equation in a form that is easy to simulate while preserving the physically important properties, such as symmetry and quantum correlations, inherent in the original equation.

At Todo Laboratory, we have been studying various quantum many-body systems ranging from quantum spin systems to real matter and even quantum computers by making full use of sampling methods such as Monte Carlo methods, representation of quantum fluctuations based on path integrals, singular value decomposition, information compression using tensor networks, statistical machine learning methods, etc. We have also been developing new techniques to simulate quantum many-body systems. We aim to elucidate the unique states, phase transitions, and dynamics of various quantum many-body systems, from quantum spin systems to real materials, and even quantum computers.

We are also developing and releasing open-source software for next-generation large-scale simulations. We are also involved in the “Quantum Software” endowed course and the “Sustainable Quantum AI” program of the JST's Co-creation Field Formation Support Program. In addition, through the “Quantum Software” endowed chair and the JST Center for Sustainable Quantum AI Research and Development, he is actively engaged in researching and developing quantum algorithms and quantum machine learning methods based on sampling and tensor networks.

Seminars

Research Highlights

Crystal structure prediction by combined optimization of experimental data and first-principles calculation

xrayCrystal structure prediction has been known as one of the most difficult problems, and various prediction methods have been developed so far. Recently, joint optimization of experimental data and the theoretical potential energy calculation has been proposed. In that method, a combined cost function, a sum of reproducibility of experimental data and the potential energy, are optimized. However, combined cost function loses the information of the local minima of each cost functions. We developed a new optimization algorithm, Combined Optimization Method (COM), to overcome this difficulty. For example, it is known that the determination of crystal structure for SiO2 systems is quite difficult due to the existence of a lot of local minimum arrangements. By using the COM, we confirmed that the success rate of crystal structure prediction increases significantly.

Non-ergodicity in Classical Harmonic Oscillator System

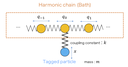ergodicity.pngUnlike the normal Langevin equation, the generalized Langevin equation, which deals with the memory effects, shows  various type diffusions depending on the memory function. Recently, the anomalous diffusion and the non-ergodicity have been actively studied in the terms of the generalized Langevin equation. There are, however, some confusions in the definition of the ergodicity and there are few analysis using physical models. We propose a new non-ergodic  model, which consists of harmonic oscillators, and analyze the model by the molecular dynamics, the exact diagonalization, and the analytical solution. We also reconsider the definition of the ergodicity, and clarify that the non-ergodicity observed in our model is caused by the localized mode.

  • Fumihiro Ishikawa, Synge Todo, Localized Mode and Nonergodicity of a Harmonic Oscillator Chain, preprint: arXiv:1805.02923.

Machine learning for molecular dynamics with strongly correlated electrons

g_r.jpgMachine learning (ML) is emerging as a promising tool to help model various types of many-body phenomena. A promising research area is the molecular dynamics (MD) of strongly correlated electron materials. While quantum MD methods based on the density functional theory have been successfully applied to a wide variety of materials, they have limited validity in their treatment of electron correlations. On the other hand, most of the many-body techniques, such as the dynamical mean-field theory, are computationally too costly for MD simulations. We showed that ML can be effective for building fast, linear-scaling MD potentials that capture correlated electron physics. Specifically, we used ML to enable large-scale Gutzwiller MD simulations of a liquid Hubbard model and studied the Mott metal-insulator transition. For the systems considered in the present study, ML is up to 6 orders of magnitude faster than direct quantum calculations. Our work opens a path toward a large-scale dynamical simulation of realistic models of correlated materials.