連続空間における経路積分モンテカルロ法

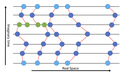He4の2次元系は低温で並進対称性とゲージ対称性が同時に破れ、超固体と呼ばれる量子相へ転移することが予想されている。有限温度での2次元系He4の平衡分布を調べ超固体の予想を裏付けるため、連続空間における経路積分モンテカルロ法の改良を進めている。Event-chainモンテカルロの手法と、worm algorithm の手法を援用し、詳細釣り合い条件を破るアルゴリズムを開発した。このアルゴリズムを相互作用のない理想Bose粒子に適用し、従来の方法より分布の収束が速く、トロッター数に対する時間計算量が改善した結果を得た。