2018

近年ノイズがありスケールしない量子コンピュータと古典コンピュータを組み合わせて計算を行う量子古典ハイブリッドアルゴリズムが注目されている。ハミルトニアンの基底状態を求める変分量子固有値ソルバー(VQE)はその代表例である。その他にも量子化学計算や組合せ最適化などの分野で幅広い応用が考えられている。我々は、励起状態を効率的に計算する部分空間変分量子固有値ソルバーを提案した。この手法により、VQEの適用範囲を励起状態およびそれに関連する特性まで広げることができる。加えて、量子古典ハイブリッドアルゴリズム内部で使用する新しい最適化アルゴリズムを提案した。これは、量子古典ハイブリッドアルゴリズムに用いる変分量子回路のパラメータに対する出力特性を活かした最適化アルゴリズムであり、検証実験ではVQEにおいて一般的に使われている最適化アルゴリズムを大きく超える性能を示した。これらのアルゴリズムは、量子古典ハイブリッドアルゴリズムの実用化を大きく加速すると期待できる。

• Ken M. Nakanishi, Kosuke Mitarai, Keisuke Fujii,
  Subspace-search variational quantum eigensolver for excited states,
  preprint: arXiv:1810.09434.
• Ken M. Nakanishi, Keisuke Fujii, Synge Todo,
  Sequential minimal optimization for quantum-classical hybrid algorithms,
  preprint: arXiv:1903.12166.

近年、機械学習を用いた第一原理的計算の高速化・大規模化が大きな注目を浴びている。多くの現実的な物理系の計算では、電子相関が重要となり計算コストが高くなるため、構造最適化が困難な問題となっている。そこで我々は強相関電子系にグッツウィラー近似を用いたイオンポテンシャルを機械学習し、分子動力学による構造最適化を可能とした。その結果、直接計算が困難な 2700 原子系に対して、100万倍程度の高速化を実現した。この新しいアプローチを用いて、連続空間上のハバード模型における金属・モット絶縁体クロスオーバーを明らかにした。機械学習による高速化は様々な手法と組み合わせることが可能で、本研究は大規模強相関電子系計算の先駆的研究と言える。

• Hidemaro Suwa, Justin S. Smith, Nicholas Lubbers, Cristian D. Batista, Gia-Wei Chern, and Kipton Barros Machine learning for molecular dynamics with strongly correlated electrons (preprint: arXiv:1811.01914)

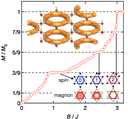相互作用にフラストレートションが存在するフラストレート磁性体は、基底状態のみならず磁場中でも興味深い秩序を示す。我々は、フラストレートした相互作用を持つS=1/2正方格子ハイゼンベルグ磁性体と考えられる電荷移動塩において、飽和磁化の1/2の磁化近傍で、大きな量子ゆらぎが生じる事を明らかにした。さらに、テンソルネットワーク変分法により、この大きな量子ゆらぎは、この物質近傍の理想化された模型で生じる、磁化プラトーが起源となっていることを示した。また、カゴメ格子S=1/2反強磁性体、Cd-kapellasitedsでは、磁場中で複数の磁化プラトーが生じ、それらはマグノンが様々な結晶格子を形成したものとして理解できることを明らかにした。

• H. Yamaguchi, Y. Sasaki, T. Okubo, M. Yoshida, T. Kida, M. Hagiwara, Y. Kono, S. Kittaka, T. Sakakibara, M. Takigawa, Y. Iwasaki, Y. Hosokoshi,
  Field-enhanced quantum fluctuation in an S=1/2 frustrated square lattice,
  Phys. Rev. B 98, 094402 (6pp) (2018). (preprint: arXiv:1808.06812)
• R. Okuma, D. Nakamura, T. Okubo, A. Miyake, A. Matsuo, K. Kindo, M. Tokunaga, N. Kawashima, S. Takeyama, Z. Hiroi,
  A series of magnon crystals appearing under ultrahigh magnetic fields in a kagomé antiferromagnet,
  Nat. Comm. 10, 1229 (7pp) (2019).

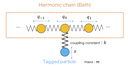記憶を含んだランジュバン方程式である一般化ランジュバン方程式は、通常のランジュバン方程式と異なり、その記憶効果によって特異な拡散現象を示すことが知られている。近年、異常拡散の解析で活発に利用され、またこの異常拡散の示す非エルゴード性が注目を集めている。しかしながら、従来の研究ではエルゴード性の定義について混乱があり、また具体的な物理的モデルを用いた解析は少なく、その物理的意味は明らかではなかった。我々は、非エルゴード性を示す古典調和振動子系を提案し、系における注目粒子の振る舞いを、分子動力学計算、厳密対角化、解析計算を用いて調べた。また同時に、エルゴード性の定義について再考した。その結果、本モデルにおける非エルゴード性の起源は注目粒子の周りに励起される孤立局在モードであることが明らかとなった。

• Fumihiro Ishikawa, Synge Todo, Localized mode and nonergodicity of a harmonic oscillator chain, Phys. Rev. E 98, 062140 (8pp) (2018). (preprint: arXiv:1805.02923)

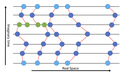He4の2次元系は低温で並進対称性とゲージ対称性が同時に破れ、超固体と呼ばれる量子相へ転移することが予想されている。有限温度での2次元系He4の平衡分布を調べ超固体の予想を裏付けるため、連続空間における経路積分モンテカルロ法の改良を進めている。Event-chainモンテカルロの手法と、worm algorithm の手法を援用し、詳細釣り合い条件を破るアルゴリズムを開発した。このアルゴリズムを相互作用のない理想Bose粒子に適用し、従来の方法より分布の収束が速く、トロッター数に対する時間計算量が改善した結果を得た。

マルコフ連鎖モンテカルロ法は高次元系における物理量を計算する手法として古くから用いられているが，次の状態への遷移確率の選び方によって物理量の推定誤差が大きく変わる。最近では棄却率最小化や詳細つりあい破れといった方法が提案されている。我々は、物理量の自己相関を陽に減らす新しい局所更新法を提案した。この方法には、物理量の推定誤差が小さくなる理由を定性的に説明できるという利点がある。また、従来の方法に比べて物理量の推定誤差が実際に小さくなることを実際のモンテカルロシミュレーションにより確認した。

ランダム磁場イジング模型(RFIM)では、ランダム性のない純粋系と比較して有効次元の低い系に相当する臨界現象が現れることが知られている。さらに、ランダム場が独立ではなくべき的(減衰指数ρ)な相関を持つ場合においてはD=d-ρで表されるD次元非相関ランダム系に相当する振る舞いとなる事がくりこみ理論により予想されている。我々は、3次元及び4次元の空間的相関をもつRFIMの臨界的振る舞いを、モンテカルロシミュレーションを用いて数値的に評価した。その結果、上部臨界次元と下部臨界次元の中間領域において、有効次元が指数ρに比例して変化する様子が示唆された。さらに、ランダム場の相関が強くなるほど系の有効次元が下部臨界次元に近づき、物理量の有限サイズ効果が顕在化だけでなく、同時に比熱に新たなピーク構造が現れるなど、これまで予想されていなかった特異な振る舞いが明らかとなった。

強相関量子多体系の研究において、数値対角化法は最も基本的かつ最も汎用性の高い手法として幅広く使われている。しかしながらその一方で、必要となるメモリ量や計算時間が系のサイズに対して指数関数的に爆発するため、その利用範囲は限られてきた。我々は、並列計算機の進歩や、新しい量子統計力学の計算手法を取り入れた現代的な量子格子模型ソルバー「HΦ」を開発・公開してきた。この並列厳密対角化パッケージでは、ハイゼンベルグ模型やハバード模型、近藤格子模型など、幅広い格子模型を解析することが可能となっている。また、従来のランチョス法による基底状態の計算だけでなく、熱的純粋量子状態を用いた比熱や構造因子の温度依存性やシフト型クリロフ部分空間法を用いた高速かつ安定した励起スペクトル計算も可能となっている。シフト型クリロフ部分空間法のルーチンについては、「Kω」という独立した数値ライブラリとしても整備・公開した。

• Mitsuaki Kawamura, Kazuyoshi Yoshimi, Takahiro Misawa, Youhei Yamaji, Synge Todo, Naoki Kawashima, Quantum Lattice Model Solver HΦ, Comp. Phys. Comm 217, 180-192 (2017). (preprint: arXiv:1703.03637)
• 山地洋平, 三澤貴宏, 吉見一慶, 河村光晶, 藤堂眞治, 川島直輝, 量子格子模型の汎用数値対角化パッケージHΦ -スピン液体近傍の熱・スピン励起へ の適用-, 固体物理 52, 539-550 (2017).