幾何学的割り当て法によるワームアルゴリズムの改良

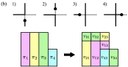worm-Ising.jpgモンテカルロ法では和をとるべき「状態」に制約があり、制約を満たしながらサンプリングすることが難しい場合があります。（例として、充足可能性問題。）そのような状況でうまく状態を変えてサンプリングする方法として代表的なのが、ワームアルゴリズム（worm algorithm）と呼ばれる手法です。ワームとは制約を破るキンク（点）のことで、ワームアルゴリズムのアイデアは「制約を常に満たすのは難しいから、いったん制約を破ってしまって後でつじつまを合わせよう」というものです。このモンテカルロ法では制約を破るワーム（キンク）を導入して、ワームを確率的に動かすことでサンプリングを行います。従来の方法では、ワームをほぼ完全にランダムに動かすようにしていました。そこで我々は効率の良い計算をするためのワームの動かし方に関する指針——できるだけ前へ進めという指針——を提案しました。これを可能にするためには、ワームが動く確率を最適化する必要があるのですが、以前我々が開発した確率最適化アルゴリズム Phys. Rev. Lett. 105, 120603 (2010) を使うと簡単に実装できます。そうして最適化したワームアルゴリズムを制約つき問題に書き直したイジングモデルに応用し、従来のワームアルゴリズムと比較して計算効率を２５倍改善しました。これはイジングモデルに対して最も効率的だと信じられているクラスターアップデートよりもさらに効率的です。