2020

近年注目を浴びている 5d 軌道の電子系では電子間相互作用とスピン軌道相互作用の両方が重要になります。我々はスピンと軌道が強く相互作用する場合、電子間のクーロン相互作用が励起子（電子と正孔の結合状態）を安定化させボーズ・アインシュタイン凝縮を引き起こすことを示しました。このように励起子のボーズ・アインシュタイン凝縮により生じる絶縁体相は励起子絶縁体と呼ばれ、現実の物質ではこれまでほとんど見つかっていませんでした。今回提案した理論を 5d 軌道の電子系であるイリジウム酸化物に適用し、２層系が長い間探されてきた励起子絶縁体であることを予言しました。またこの２層系の物質は、励起子がボーズ・アインシュタイン凝縮を起こす量子相転移のすぐ近くにあることを理論的に見出しました。相対論の効果でスピンと軌道が強く相互作用する 5d 電子系では、電子間のクーロン相互作用と電子の運動エネルギーが同程度であることが本質的に重要となることを示しました。

• Hidemaro Suwa, Shang-Shun Zhang, Cristian D. Batista, Exciton condensation in bilayer spin-orbit insulator, Phys. Rev. Research 3, 013224 (2021).

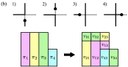モンテカルロ法では和をとるべき「状態」に制約があり、制約を満たしながらサンプリングすることが難しい場合があります。（例として、充足可能性問題。）そのような状況でうまく状態を変えてサンプリングする方法として代表的なのが、ワームアルゴリズム（worm algorithm）と呼ばれる手法です。ワームとは制約を破るキンク（点）のことで、ワームアルゴリズムのアイデアは「制約を常に満たすのは難しいから、いったん制約を破ってしまって後でつじつまを合わせよう」というものです。このモンテカルロ法では制約を破るワーム（キンク）を導入して、ワームを確率的に動かすことでサンプリングを行います。従来の方法では、ワームをほぼ完全にランダムに動かすようにしていました。そこで我々は効率の良い計算をするためのワームの動かし方に関する指針——できるだけ前へ進めという指針——を提案しました。これを可能にするためには、ワームが動く確率を最適化する必要があるのですが、以前我々が開発した確率最適化アルゴリズム Phys. Rev. Lett. 105, 120603 (2010) を使うと簡単に実装できます。そうして最適化したワームアルゴリズムを制約つき問題に書き直したイジングモデルに応用し、従来のワームアルゴリズムと比較して計算効率を２５倍改善しました。これはイジングモデルに対して最も効率的だと信じられているクラスターアップデートよりもさらに効率的です。

• Hidemaro Suwa, Geometric allocation approach to accelerating directed worm algorithm, Phys. Rev. E 103, 013308 (2021). (preprint: arXiv:1703.03136)

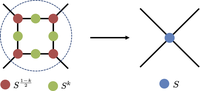テンソルネットワークを用いた実空間くりこみ群法は、多体スピン系に対する数値計算手法として近年広く用いられてきている。テンソルくりこみ群法では大規模な古典系/量子系の物理量を効率的に計算することができる。しかしながら、Tensor Renormalization Group (TRG)やHigher-Order Tensor Renormalization Group (HOTRG)といった既存の手法では、高次元になるほど計算量が膨大になってしまうという問題点があった。この問題を解決するために、既存手法に比べて計算量が低い手法や、同じ計算時間でより精度の高い複数の手法を開発してきた。我々の提案したAnisotropic Tensor Renormalization Group (ATRG)では、3次元量子系など高次元系における計算量を劇的に減らすことができる。さらに、テンソルネットワークをテンソルを頂点上だけでなく頂点を結ぶ線上にも置いた形に拡張することで、実空間くりこみ法の精度を、既存の同程度の計算時間を要する数値計算手法に比べて100倍程度高めることに成功した。この手法は一般のテンソルネットワークに対して適用可能である。また、ランダム系やフラストレート古典スピン系へのテンソルネットワークの応用についても研究を進めている

• Daiki Adachi, Tsuyoshi Okubo, Synge Todo, Anisotropic tensor renormalization group, Phys. Rev. B 102, 054432 (7pp) (2020). (preprint: arXiv:1906.02007)
• Daiki Adachi, Tsuyoshi Okubo, Synge Todo, Bond-weighted Tensor Renormalization Group, preprint: arXiv:2011.01679

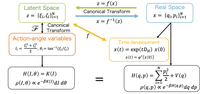可積分系は物理と数学において豊富な知見を提供してきた。特に古典可積分系は古くから研究されながらも、今なお多くの新たな発見が報告されている。これまで、古典可積分系は、偶然あるいはひらめきによって、あるいはある種の仮設の範囲でのみ発見・構成されてきた。我々はこれに対し、深層学習を用いることで、これまでにない新たな構成法を提案した。具体的には、「作用角変数」と呼ばれる特殊な正準座標で与えられたハミルトニアンを与え、それに対する自然なハミルトニアンを深層学習によって発見する。この手法では特に、(i) ニューラルネットで全単射な座標変換を表現できる。(ii) 時間発展の自動微分を随伴法により効率化できる点に着目した。実際に古典可積分系の代表である戸田格子に対して我々の手法を適用し、戸田格子のポテンシャルを見つけ出すことができることを示した

• Fumihiro Ishikawa, Hidemaro Suwa, Synge Todo, Neural Network Approach to Construction of Classical Integrable Systems, preprint: arXiv:2103.00372.

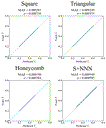イジングモデルの臨界温度決定問題について、これまで近似を用いる手法や計算機で数値的に解く手法が主流であった。我々は、異なるアプローチとして、ニューラルネットワークを用いる手法を提案した。格子の特徴量として格子グリーン関数を用いることで、異なる構造の格子に対して共通のニューラルネットワークを用いて臨界温度を予測することが可能となる。4種類の格子を用いテストを行った結果、学習データに含めた格子については高い精度で臨界温度予測に成功した。また学習データに含めていない格子についても、部分的ではあるが、臨界温度の予測が可能であることを示した

近年、量子コンピュータによる量子状態計算と古典計算機による最適化を組み合わせて計算を行う量子古典ハイブリッドアルゴリズムが注目されている。量子古典ハイブリッドアルゴリズムの応用先は、量子化学計算や組合せ最適化、量子機械学習など多岐にわたる。これらのアルゴリズムでは、変分量子回路を用いて計算されたコスト関数が最小になるように変分量子回路のパラメータを最適化する。我々は、変分量子回路のパラメータ最適化のための手法として、逐次最小問題最適化法を提案した。変分量子回路の最適化問題は、解析的に最小値を求められる部分問題に分割できる。具体的には、変分量子回路のパラメータの中から 1 つを選択し、それ以外のパラメータを固定すると、コスト関数は周期$2\pi$の三角関数となっているので、そのパラメータに関して最小値を厳密に求めることができる。この部分問題を繰り返し解くことにより、コスト関数を最小化するように変分量子回路を最適化できる。提案手法を既存の最適化アルゴリズムと比較した結果、提案手法は既存のアルゴリズムよりもはるかに収束が速く、統計誤差に対して頑健であることが明らかとなった。また、提案手法はハイパーパラメータを持たないという点でも利用しやすいアルゴリズムとなっている。提案手法はあらゆる量子古典ハイブリッドアルゴリズムの高速化の目的で容易に導入することが可能であり、量子コンピュータの利用において重要なツールとなると期待される

• Ken M. Nakanishi, Keisuke Fujii, Synge Todo, Sequential minimal optimization for quantum-classical hybrid algorithms, Phys. Rev. Research 2, 043158 (10pp) (2020). (preprint: arXiv:1903.12166)

孤立量子系の研究において、ランダムネスによって励起状態の性質が転移することが注目されている。ランダムネスの弱いときは非局在状態、強いときは局在状態が現れ、多体局在現象(many-body localization)と呼ばれている。我々は、その転移点を求めるため、ハミルトニアンの疎性を用いて任意のターゲット付近の固有ベクトルを高速に求めるSI Lanczos法を、ランダム磁場ハイゼンベルグ模型に適用し、少数の粒子系で完全対角化と同じ結果を再現できることを確かめた。また、連立一次方程式の求解にLU分解ではなくKrylov部分空間法を用いることで、ヒルベルト空間の次元のオーダーの空間計算量で固有ベクトルを求めることができるようになった

非平衡環境下における開放量子多体系の熱平衡化現象について、テンソルネットワークに基づくアルゴリズムを用いた研究を行なった。孤立量子多体系の熱平衡化は固有状態熱化仮説(ETH)によって理解することができる。近年、リンドブラッド型の量子マスター方程式で記述される開放量子多体系についても、ETHに基づく議論によって熱平衡化が議論できることが明らかになった。しかし、この議論には熱力学極限と弱結合極限の交換に関する問題を含んでおり、大規模数値計算と有限サイズスケーリングに基づく検証が必要だった。テンソルネットワークによる数値計算では、並進対称性を仮定することで熱力学極限における状態を直接表現することが可能である。我々は、行列積演算子を用いて熱力学極限におけるリンドブラッド方程式の数値計算を行った。これによって、弱結合極限において系の初期状態がギブス状態であるとき、非平衡定常状態に至るまでの緩和過程の全てにおいて状態はギブス状態と区別できないことを示した

• Hayate Nakano, Tatsuhiko Shirai, Takashi Mori, Tensor-network approach to thermalization in open quantum many-body systems, Phys. Rev. E 103, L040102 (6pp) (2021). (preprint: arXiv:2012.12274)
• Tatsuhiko Shirai, Takashi Mori, Thermalization in Open Many-Body Systems Based on Eigenstate Thermalization Hypothesis, Phys. Rev. E 101, 042116 (11pp) (2020). (preprint: arXiv:1812.09713)
•  

日本国内においても、高性能な物質科学シミュレーションソフトウェアが数多く開発・公開されているが、その知名度は必ずしも高くない。また、ドキュメントの作成やユーザサポートにも問題が多く、普及の妨げとなっている。物質科学アプリケーションのさらなる公開・普及を目指し、物質科学シミュレーションのポータルサイト「MateriApps」の整備を行っている。また、気軽にシミュレーションを始めることのできる環境構築を目指し、仮想Linuxシステム「MateriApps LIVE!」、MateriAppsアプリケーションのインストールスクリプト集「MateriApps Installer」の開発・公開も進めている。

• MateriApps - 物質科学シミュレーションのポータルサイト, MateriApps LIVE!, MateriApps Installer
• 井戸康太, 加藤岳生, 三澤貴宏, 藤堂眞治, ソフトウェア紹介「物質科学シミュレーションのポータルサイトMateriApps ― 分子動力学シミュレーションのはじめの一歩, 分子シミュレーション学会誌 “アンサンブル” 22, 74-80 (2020).
• 本山裕一, 三澤貴宏, 加藤岳生, 藤堂眞治, 物質科学シミュレーションのポータルサイト MateriApps, 固体物理 52, 743-755 (2017).
• Yusuke Konishi, Ryo Igarashi, Shunsuke Kasamatsu, Takeo Kato, Naoki Kawashima, Tsutomu Kawatsu, Hikaru Kouta, Masashi Noda, Shoichi Sasaki, Yayoi Terada, Syng e Todo, Shigehiro Tsuchida, Kazuyoshi Yoshimi, Kanako Yoshizawa, MateriApps --- a Portal Site of Materials Science Simulation, JPS Conf. Proc. 5, 011007 (2015).
• 平成31年度文部科学大臣表彰 http://www.mext.go.jp/b_menu/houdou/31/04/1415044.htm
• 理学系研究科のページ https://www.s.u-tokyo.ac.jp/ja/info/6354/

量子多体系の状態を表すベクトル(状態ベクトル)の次元は、粒子数に対して指数関数的に増大するため、大きな量子多体系を計算機を用いて解析するには、状態ベクトルの情報を効率的を圧縮し、精度良く近似することが有用である。そのような情報圧縮法の一つであるテンソルネットワーク法は、特に相互作用にフラストレーションの存在する量子スピン系の解析に対して強力な方法である一方、これまでに、一般的な模型に簡単に適用できるシミュレーションソフトウェアは存在しなかった。我々は、任意の2次元格子上のスピン模型に対してテンソルネットワーク法を適用して基底状態を計算できるソルバー「TeNeS」を開発・公開した。また、量子モンテカルロ法など量子格子模型のための汎用シミュレーションソフトウェアALPSや並列厳密対角化パッケージHΦなどの公開・開発も行っている

• TeNeS
• ALPS
• HΦ

BLISは米国テキサス大SHPC研が開発している柔軟かつ高速的な行列演算ライブラリーである。標準のBLASとの互換性を保っており、AMDの公式BLASとして採用されている。BLISは最小限のコーディングから最大性能を引き出すことで知られており、様々なプラットフォームにおいて公式のBLASを凌ぐ性能を発揮する。BLIS はCで書かれたフレーム部分とそれぞれのCPUアーキテクチャに特化したアセンブラカーネルから構成され、そのアセンブラ部分こそがBLIS高速化の鍵となっている。我々は、ドイツの Jülich 研と共同で、「富岳」のA64FXプロセッサに最適化したBLISのアセンブラカーネルを開発した。現在、富岳の1ノードにおいて、BLISの性能は理論ピークの75%を実現しており、これはArmPLや富士通SSL2(2021年2月版)をも凌いでいる。今後、90%以上のピーク性能を目指し、さらにチューニングを進める予定である

• BLIS

多変数変分モンテカルロ法mVMCは、日本の物性理論コミュニティーにおいて広く使われ、これまで、強相関電子系の基底状態状態における様々な性質(磁性、超伝導など)を解き明かしてきた。しかし、mVMCにおける演算のホットスポットは、反対称逆行列 X^-1のRank-1更新であるため、現代のプロセッサーにおいては、性能を発揮することは難しい。「富岳」の新プロセッサA64FXにおいてmVMCの性能を充分に発揮するため、我々は、Woodbury公式を使って更新式を書き直し、Rank-1更新を Rank-k更新に置き換えた。これにより「富岳」における mVMC の性能を大幅に向上することができた

• RuQing G. Xu, Tsuyoshi Okubo, Synge Todo, Masatoshi Imada, Optimized Implementation for Calculation and Fast-Update of Pfaffians Installed to the Open-Source Fermionic Variational Solver mVMC, preprint: arXiv:2105.13098.