ニューラルネットを用いた古典可積分系の構成

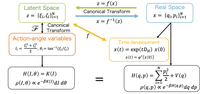可積分系は物理と数学において豊富な知見を提供してきた。特に古典可積分系は古くから研究されながらも、今なお多くの新たな発見が報告されている。これまで、古典可積分系は、偶然あるいはひらめきによって、あるいはある種の仮設の範囲でのみ発見・構成されてきた。我々はこれに対し、深層学習を用いることで、これまでにない新たな構成法を提案した。具体的には、「作用角変数」と呼ばれる特殊な正準座標で与えられたハミルトニアンを与え、それに対する自然なハミルトニアンを深層学習によって発見する。この手法では特に、(i) ニューラルネットで全単射な座標変換を表現できる。(ii) 時間発展の自動微分を随伴法により効率化できる点に着目した。実際に古典可積分系の代表である戸田格子に対して我々の手法を適用し、戸田格子のポテンシャルを見つけ出すことができることを示した