変分量子回路パラメータ最適化のための逐次最小問題最適化法

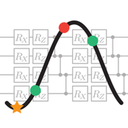optimization.png近年、量子コンピュータによる量子状態計算と古典計算機による最適化を組み合わせて計算を行う量子古典ハイブリッドアルゴリズムが注目されている。量子古典ハイブリッドアルゴリズムの応用先は、量子化学計算や組合せ最適化、量子機械学習など多岐にわたる。これらのアルゴリズムでは、変分量子回路を用いて計算されたコスト関数が最小になるように変分量子回路のパラメータを最適化する。我々は、変分量子回路のパラメータ最適化のための手法として、逐次最小問題最適化法を提案した。変分量子回路の最適化問題は、解析的に最小値を求められる部分問題に分割できる。具体的には、変分量子回路のパラメータの中から 1 つを選択し、それ以外のパラメータを固定すると、コスト関数は周期$2\pi$の三角関数となっているので、そのパラメータに関して最小値を厳密に求めることができる。この部分問題を繰り返し解くことにより、コスト関数を最小化するように変分量子回路を最適化できる。提案手法を既存の最適化アルゴリズムと比較した結果、提案手法は既存のアルゴリズムよりもはるかに収束が速く、統計誤差に対して頑健であることが明らかとなった。また、提案手法はハイパーパラメータを持たないという点でも利用しやすいアルゴリズムとなっている。提案手法はあらゆる量子古典ハイブリッドアルゴリズムの高速化の目的で容易に導入することが可能であり、量子コンピュータの利用において重要なツールとなると期待される