2017

一次元のSPT相に対しては、ストリング秩序変数、ひねり秩序変数など、トポロジカルな秩序を特徴づける様々な隠れた秩序変数が提案され、数値シミュレーションでもその正当性が検証されている。しかしながら、二次元以上においてSPT相が存在するかどうか、さらにそれを特徴づけるトポロジカル秩序変数は何か、など未解明の問題も多い。我々は、近年提案されたstrange correlatorと呼ばれる相関関数を量子モンテカルロ法を用いて精度良く計算する手法を開発した。また、一次元系において、strange correlatorがSPT相を正しく特徴付けることを確認した。この手法は二次元のSPT相に対しても同様に適用可能である。

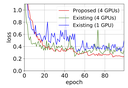近年、深層学習において、複数のGPUを使って学習を分散処理するときのGPU間の通信量が大きな課題となっている。一般的なデータ並列による分散処理では、最新のニューラルネットの構成を用いると一回の更新あたり数十〜数百MBに及ぶ通信が発生する。そのため、分散処理による学習時はこの通信にかかる時間がボトルネックとなってしまうことが多い。我々はGPU間での通信量を大幅に減らす方法を提案した。これを用いると、分散処理をしてもGPU間の通信速度に依らず高速に学習することが示された。

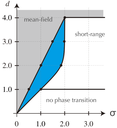長距離相互作用を持つスピン系は、近接相互作用のみの系とは異なった臨界現象を示すことが知られている。しかしながら、平均場的領域、中間領域、近接的領域、それぞれの境界については、これまで明らかではなかった。我々は、べき的に減衰する長距離相互作用を持つ二次元正方格子イジング模型を、オーダーNクラスターアルゴリズムを用いてシミュレーションを行い、臨界指数と臨界係数を精度よく評価した。また、"combined Binder ratio"'と呼ばれる、スケーリング補正項を打ち消すユニバーサルな方法を開発し、境界領域における相転移の臨界指数の振る舞いを明らかにした。

• Toshiki Horita, Hidemaro Suwa, Synge Todo, Upper and lower critical decay exponents of Ising ferromagnet with long-range interaction, Phys. Rev. E 95, 012143 (2017). (preprint: arXiv:1605.09496)

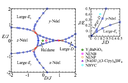S=1の反強磁性スピン鎖におけるハルデン相は対称性に保護されたトポロジカル(SPT)相の代表例である。実際の物質において、このようなスピン系を考える場合、一軸異方性 D(Sz)^2やrhombic異方性E((Sx)^2-(Sy)^2)という1イオン異方性を考慮した基底状態の理解が重要になる。これまでは主に、一軸異方性の影響を中心に研究が行われ、ハルデン相の他にS_zの反強磁性秩序相、Large-D相が存在することが知られていた。我々は、密度行列繰り込み群法を用いて、rhombic異方性も考慮した場合の基底状態相図を明らかにし、わずかでもrhombic異方性が存在すると、ハルデン相とLarge-D相の間に中間相(SxまたはSyの反強磁性秩序相)が生じることを示した。また、エネルギー準位の交差により相転移点を決定するレベルスペクトロスコピーにより、rhombic異方性がない場合のハルデン相とLarge-D相の相境界を6桁の精度で精密に決定した。

• Yu-Chin Tzeng, Hiroaki Onishi, Tsuyoshi Okubo, Ying-Jer Kao, Quantum phase transitions driven by rhombic-type single-ion anisotropy in the S = 1 Haldane chain, Phys. Rev. B 96, 060404(R) (2017).