藤堂研究室へようこそ
シミュレーションで探る量子多体現象
物質の状態を知るには、多体のシュレディンガー方程式を解き、統計力学の分配関数を求めればよい。しかしながら、現代のスーパーコンピュータの計算能力をもってしても、完全な解を求めることは不可能である。そこで、対称性や量子相関など、もとの方程式の中に含まれている物理的に重要な性質を失うことなく、シミュレーションを実行しやすい形へ表現しなおすことが、計算物理における重要な鍵となる。
藤堂研究室では、モンテカルロ法などのサンプリング手法、経路積分に基づく量子ゆらぎの表現、特異値分解やテンソルネットワークによる情報圧縮、統計的機械学習の手法などを駆使し、量子スピン系から現実の物質にいたるまで、さまざまな量子多体系に特有の状態、相転移現象、ダイナミクスの解明を目指している。さらに、量子コンピュータの基礎理論や量子機械学習アルゴリズムの研究、次世代シミュレーションのためのオープンソースソフトウェアの開発・公開も進めている。
セミナー
- 統計力学セミナー @ 本郷 理学部
- ipi seminar
- 計算科学フォーラム
最近の研究より
- 藤堂研究室発表論文リスト(2002-)
多変数変分モンテカルロ法mVMCの高度化
多変数変分モンテカルロ法mVMCは、日本の物性理論コミュニティーにおいて広く使われ、これまで、強相関電子系の基底状態状態における様々な性質(磁性、超伝導など)を解き明かしてきた。しかし、mVMCにおける演算のホットスポットは、反対称逆行列 X-1のRank-1更新であるため、現代のプロセッサーにおいては、性能を発揮することは難しい。「富岳」の新プロセッサA64FXにおいてmVMCの性能を充分に発揮するため、我々は、Woodbury公式を使って更新式を書き直し、Rank-1更新を Rank-k更新に置き換えた。これにより「富岳」における mVMC の性能を大幅に向上することができた
- RuQing G. Xu, Tsuyoshi Okubo, Synge Todo, Masatoshi Imada, Optimized Implementation for Calculation and Fast-Update of Pfaffians Installed to the Open-Source Fermionic Variational Solver mVMC, preprint: arXiv:2105.13098.
ニューラルネットを用いた古典可積分系の構成
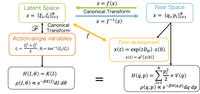 可積分系は物理と数学において豊富な知見を提供してきた。特に古典可積分系は古くから研究されながらも、今なお多くの新たな発見が報告されている。これまで、古典可積分系は、偶然あるいはひらめきによって、あるいはある種の仮設の範囲でのみ発見・構成されてきた。我々はこれに対し、深層学習を用いることで、これまでにない新たな構成法を提案した。具体的には、「作用角変数」と呼ばれる特殊な正準座標で与えられたハミルトニアンを与え、それに対する自然なハミルトニアンを深層学習によって発見する。この手法では特に、(i) ニューラルネットで全単射な座標変換を表現できる。(ii) 時間発展の自動微分を随伴法により効率化できる点に着目した。実際に古典可積分系の代表である戸田格子に対して我々の手法を適用し、戸田格子のポテンシャルを見つけ出すことができることを示した
可積分系は物理と数学において豊富な知見を提供してきた。特に古典可積分系は古くから研究されながらも、今なお多くの新たな発見が報告されている。これまで、古典可積分系は、偶然あるいはひらめきによって、あるいはある種の仮設の範囲でのみ発見・構成されてきた。我々はこれに対し、深層学習を用いることで、これまでにない新たな構成法を提案した。具体的には、「作用角変数」と呼ばれる特殊な正準座標で与えられたハミルトニアンを与え、それに対する自然なハミルトニアンを深層学習によって発見する。この手法では特に、(i) ニューラルネットで全単射な座標変換を表現できる。(ii) 時間発展の自動微分を随伴法により効率化できる点に着目した。実際に古典可積分系の代表である戸田格子に対して我々の手法を適用し、戸田格子のポテンシャルを見つけ出すことができることを示した
- Fumihiro Ishikawa, Hidemaro Suwa, Synge Todo, Neural Network Approach to Construction of Classical Integrable Systems, preprint: arXiv:2103.00372.
