2019
フェリ磁性体スピネル化合物における顕著なスピン格子結合
 これまで反強磁性体では、スピンフラストレーションとスピン格子結合の競合現象が起きることが知られていた。このような現象が他の系や物質でも生じるのかどうかは興味深い問題である。我々はフェリ磁性体スピネル化合物においても、スピン格子結合が重要な役割を担うことを明らかにした。フェリ磁性体スピネル化合物MnCr2S4の磁化曲線を110テスラの高磁場まで調べ、新たな磁場誘起相転移を発見し、磁場温度相図を決定した。また磁歪と超音波を60テスラまで測定し顕著なスピン格子結合を見出した。この物質に対する有効模型を考案し、モンテカルロ計算を用いて実験結果を高精度で再現することに成功した。実験的に観測された巨大プラトー相と非対称スピン秩序相が、スピン格子結合により安定化されることを明らかにした。我々が発見した非対称スピン秩序相ではマルチフェロイックな性質が創発されるため、今後の工学的応用が期待される。
これまで反強磁性体では、スピンフラストレーションとスピン格子結合の競合現象が起きることが知られていた。このような現象が他の系や物質でも生じるのかどうかは興味深い問題である。我々はフェリ磁性体スピネル化合物においても、スピン格子結合が重要な役割を担うことを明らかにした。フェリ磁性体スピネル化合物MnCr2S4の磁化曲線を110テスラの高磁場まで調べ、新たな磁場誘起相転移を発見し、磁場温度相図を決定した。また磁歪と超音波を60テスラまで測定し顕著なスピン格子結合を見出した。この物質に対する有効模型を考案し、モンテカルロ計算を用いて実験結果を高精度で再現することに成功した。実験的に観測された巨大プラトー相と非対称スピン秩序相が、スピン格子結合により安定化されることを明らかにした。我々が発見した非対称スピン秩序相ではマルチフェロイックな性質が創発されるため、今後の工学的応用が期待される。
- A. Miyata, H. Suwa, T. Nomura, L. Prodan, V. Felea, Y. Skourski, J. Deisenhofer, H.-A. Krug von Nidda, O. Portugall, S. Zherlitsyn, V. Tsurkan, J. Wosnitza, and A. Loidl Spin-lattice coupling in a ferrimagnetic spinel: Exotic H-T phase diagram of MnCr2S4 up to 110 T, Phys. Rev. B 101, 054432 (2020), preprint: arXiv:1911.12103
テンソルネットワークくりこみ群法の高速数値計算手法開発

テンソルネットワークを用いた実空間くりこみ群法は、多体スピン系に対する数値計算手法として近年広く用いられてきている。テンソルくりこみ群法では大規模な古典系/量子系の物理量を効率的に計算することができる。しかしながら、Tensor Renormalization Group (TRG)やHigher-Order Tensor Renormalization Group (HOTRG)といった既存の手法では、高次元になるほど計算量が膨大になってしまうという問題点があった。この問題を解決するために、既存手法に比べて計算量が低い手法や、同じ計算時間における精度の高い複数の手法を開発してきた。例えば、Anisotropic Tensor Renormalization Group (ATRG)では、三次元量子系など高次元系における計算量を劇的に減らすことができる。さらに、ボンド重みを取り入れたテンソルくりこみ群法やGraph-independent loop reduction methodsといった手法との組み合わせにより、ATRGの精度のさらなる向上を進めている。
- Daiki Adachi, Tsuyoshi Okubo, Synge Todo, Anisotropic Tensor Renormalization Group, preprint: arXiv:1906.02007.
実験データと第一原理計算を組み合わせた結晶構造決定
 結晶構造推定は非常に難しい問題として古くから知られており、様々な推定方法が開発されてきた。特に最近では、実験データがある場合にはエネルギーの最適化と実験データの再現を同時に行うことによって、結晶構造推定の成功率を上げられることが知られてきている。その際に用いられる方法は、実験データの再現度とエネルギーを足し合わせた新しい評価関数を用いて最適化を行うと言った方法である。しかしながら、2つの評価関数を 足し合わせてしまっているため、それぞれの評価関数の情報が失われてしまうといった欠点がある。我々は2つの評価関数の同時最適点を探る方法として重ね合わせ最適化法を開 発し、その性能について調査を行なっている。例えばSiO2系は、エネルギーの局所最 適点が多く存在するため結晶構造を決定するのが難しい系であるが、我々の方法を用いることで結晶構造の推定精度が大幅に上昇することことを確認した。
結晶構造推定は非常に難しい問題として古くから知られており、様々な推定方法が開発されてきた。特に最近では、実験データがある場合にはエネルギーの最適化と実験データの再現を同時に行うことによって、結晶構造推定の成功率を上げられることが知られてきている。その際に用いられる方法は、実験データの再現度とエネルギーを足し合わせた新しい評価関数を用いて最適化を行うと言った方法である。しかしながら、2つの評価関数を 足し合わせてしまっているため、それぞれの評価関数の情報が失われてしまうといった欠点がある。我々は2つの評価関数の同時最適点を探る方法として重ね合わせ最適化法を開 発し、その性能について調査を行なっている。例えばSiO2系は、エネルギーの局所最 適点が多く存在するため結晶構造を決定するのが難しい系であるが、我々の方法を用いることで結晶構造の推定精度が大幅に上昇することことを確認した。
- 藤堂眞治, 常行真司, X線回折実験とシミュレーションのデータ同化による結晶構造解析, 日本結晶学会誌 62, 51-55 (2020).
- Daiki Adachi, Naoto Tsujimoto, Ryosuke Akashi, Synge Todo, Shinji Tsuneyuki, Search for Common Minima in Joint Optimization of Multiple Cost Functions, Comp. Phys. Comm. 241, 92-97 (2019). (preprint: arXiv:1808.06846)
- Naoto Tsujimoto, Daiki Adachi, Ryosuke Akashi, Synge Todo, Shinji Tsuneyuki, Crystal structure prediction supported by incomplete experimental data, Phys. Rev. Materials 2, 053801 (2018). (preprint: arXiv:1705.08613)
キタエフスピン液体のテンソルネットワーク解析
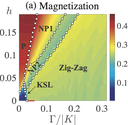
近年、強いスピン軌道相互作用の存在により、有効スピンの間に異方的なキタエフ相互作用を持つ物質群が注目を集めている。キタエフ相互作用のみが存在するハニカム格子上のS=1/2量子スピン模型(キタエフ模型)の基底状態は非磁性のスピン液体状態になっており、このような"キタエフスピン液体"が現実の物質で実現する可能性が議論されている。我々は、以前に提案したキタエフスピン液体のテンソルネットワーク表現(ループガス状態)を拡張することで、スター格子と呼ばれる格子上でのキタエフ模型の基底状態相図を計算した。その結果、ループガス状態は、「カイラルスピン液体」と呼ばれるスピン液体をを定性的・定量的に表現することができ、さらに、異なるカイラルスピン液体(AbelianとNon-Abelian)の間の相転移も表現できることを明らかにした。また、RuCl3の有効模型に対する磁場中基底状態の解析にもテンソルネットワーク表現を適用し、磁場の印加によりゼロ磁場での磁性状態が抑制されて、非磁性状態が安定化することを明らかにした。
- Hyun-Yong Lee, Ryui Kaneko, Li Ern Chern, Tsuyoshi Okubo, Youhei Yamaji, Naoki Kawashima, Yong Baek Kim, Magnetic field induced quantum phases in a tensor network study of Kitaev magnets, Nat. Comm. 11, 1639 (7pp) (2020). (preprint: arXiv:1908.07671)
- Hyun-Yong Lee, Ryui Kaneko, Tsuyoshi Okubo, Naoki Kawashima, Abelian and Non-Abelian Chiral Spin Liquids in a Compact Tensor Network Representation, Phys. Rev. B 101, 035140 (9pp) (2020). (preprint: arXiv:1907.02268)
- Tsuyoshi Okubo, Kazuya Shinjo, Youhei Yamaji, Naoki Kawashima, Shigetoshi Sota , Takami Tohyama, Masatoshi Imada,
Ground-state properties of Na2IrO3 determined from an ab initio Hamiltonian and its extensions containing Kitaev and extended Heisenberg interactions,
Phys. Rev. B 96, 054434 (2017)
共振器系での動的な協力現象
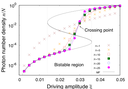 レーザー照射下で現れる光双安定性は、レーザー強度に対して共振器中のフォトン数が双安定な状態を示し、またその間を不連続に跳ぶといった一次相転移現象に似た振る舞いの現れる相転移現象である。このような非平衡系で現れる動的な協力現象を、大規模な数値計算によって量子力学的な微視的模型から解析を行った。具体的には多数のフォトンと多数の二準位原子からなる量子マスター方程式を近似なく解く並列計算を実行した。量子マスター方程式の時間発展演算子の固有値・固有状態から、定常状態でのフォトン数分布関数のサイズ依存性、および緩和時間のサイズ依存性を調べ、平衡系での一次相転移に対応する結果を得た。従来の研究と比べフォトン数密度の小さな領域では、準安定状態のレーザー周波数依存性が定性的に異なることを明らかにした。また、レーザー強度を時間周期的に変調させることで、その周期に対し動的な相転移現象が現れることを明らかにした。
レーザー照射下で現れる光双安定性は、レーザー強度に対して共振器中のフォトン数が双安定な状態を示し、またその間を不連続に跳ぶといった一次相転移現象に似た振る舞いの現れる相転移現象である。このような非平衡系で現れる動的な協力現象を、大規模な数値計算によって量子力学的な微視的模型から解析を行った。具体的には多数のフォトンと多数の二準位原子からなる量子マスター方程式を近似なく解く並列計算を実行した。量子マスター方程式の時間発展演算子の固有値・固有状態から、定常状態でのフォトン数分布関数のサイズ依存性、および緩和時間のサイズ依存性を調べ、平衡系での一次相転移に対応する結果を得た。従来の研究と比べフォトン数密度の小さな領域では、準安定状態のレーザー周波数依存性が定性的に異なることを明らかにした。また、レーザー強度を時間周期的に変調させることで、その周期に対し動的な相転移現象が現れることを明らかにした。
- Tatsuhiko Shirai, Synge Todo, Seiji Miyashita, Dynamical phase transition in Floquet optical bistable systems: An approach from finite-size quantum systems, Phys. Rev. A 101, 013809 (7pp) (2020). (preprint: arXiv:1910.10618)
- Tatsuhiko Shirai, Synge Todo, Hans de Raedt, Seiji Miyashita, Optical bistability in a low-photon-density regime, Phys. Rev. A 98, 043802 (13pp) (2018). (preprint: arXiv:1804.09853)
非一様な系に対するテンソルネットワーク繰り込み
テンソルネットワークは、厳密対角化といった従来の指数的にコストがかかる計算手法に比べ、ベキ的な計算量のコストですむ計算手法として近年注目されている。代表的な手法にTRGや、HOTRGといったものがあるが、それ以外にProjectorによる手法も注目されている。これまでテンソルネットワークは一様な系に対して用いられてきたが、我々は、HOTRGとProjectorによる計算手法を非一様系に拡張し、ボンド希釈を含むイジングモデルに適用し、非一様系においてProjectorによる手法が収束が速いことを確認した
量子モンテカルロ法によるRényiエンタングルメントエントロピーの測定
 エンタングルメントエントロピーは、量子多体系における量子相関を表す指標のひとつであり、特に基底状態におけるエンタングルメントエントロピーを秩序変数とみなすことで量子相転移を特徴付けることが出来る。一方、量子多体系を解析する上で強力な計算手法として虚時間経路積分に基づく有限温度量子モンテカルロ法が従来より用いられてきたが、相関長が有限の場合においては絶対零度(基底状態)を直接サンプリングすることも可能である。この基底状態をサンプリングする量子モンテカルロ法とレプリカ法を組み合わせることで基底状態のRényiエントロピーを直接計算する手法を開発した。
エンタングルメントエントロピーは、量子多体系における量子相関を表す指標のひとつであり、特に基底状態におけるエンタングルメントエントロピーを秩序変数とみなすことで量子相転移を特徴付けることが出来る。一方、量子多体系を解析する上で強力な計算手法として虚時間経路積分に基づく有限温度量子モンテカルロ法が従来より用いられてきたが、相関長が有限の場合においては絶対零度(基底状態)を直接サンプリングすることも可能である。この基底状態をサンプリングする量子モンテカルロ法とレプリカ法を組み合わせることで基底状態のRényiエントロピーを直接計算する手法を開発した。
量子ダイマー模型における非局所更新モンテカルロ法
量子ダイマー模型は1988年にRokhsarとKivelsonによりフラストレートした磁性体の低エネルギー有効模型として提案された。量子ダイマー模型のハミルトニアンには負符号問題はないが、ダイマーの配置に強い幾何学的な制限があるため、モンテカルロシミュレーションは非常に困難であった。近年、2次元量子ダイマー模型に対して、Stochastic Series Expansion法に基づく新しい量子モンテカルロ法が提案されたが、さらに、新しいデータ構造を取り入れることで、より効率よく有限温度のシミュレーションを行うことが可能となった。この新しい非局所更新モンテカルロ法と有限サイズスケーリングを組み合わせることで、2次元量子ダイマー模型の有限温度相図を精密に決定した。
機械学習を用いた高ヤング率材料探索
 機械学習、特にベイズ推定などを用いた統計的手法による新材料探索(マテリアルズインフォマティクス)が注目を浴びている。機械学習を用いることで、既存物質データを元により性能の高い新物質を予測し、探索することが可能となると期待されている。我々は、特にベイズ最適化を用いた手法を応用し、高ヤング率材料の候補となる物質を探索し、第一原理計算によってそのヤング率を調べた。結果、ベイズ推定とベイズ最適化を用いることで、非常に少ない回数で探索範囲内の最も高いヤング率を示す材料を発見することができた。
機械学習、特にベイズ推定などを用いた統計的手法による新材料探索(マテリアルズインフォマティクス)が注目を浴びている。機械学習を用いることで、既存物質データを元により性能の高い新物質を予測し、探索することが可能となると期待されている。我々は、特にベイズ最適化を用いた手法を応用し、高ヤング率材料の候補となる物質を探索し、第一原理計算によってそのヤング率を調べた。結果、ベイズ推定とベイズ最適化を用いることで、非常に少ない回数で探索範囲内の最も高いヤング率を示す材料を発見することができた。
